prima relazione fondamentale della goniometria

Relazioni fondamentali della goniometria Prima relazione fondamentale Da questa si ricavano Ricordare di valutare la posizione di per la scelta opportuna del segno. Consideriamo adesso anche la tangente.

Prima Relazione Fondamentale Della Goniometria

In questa pagina sono elencate le identità o relazioni fondamentali della goniometria.

. Relazioni fondamentali della goniometria sin 2 α cos 2 α 1 tan α sin α cos α Significato geometrico delle funzioni goniometriche Muovi il punto P per vedere come variano le. Teorema 51 Prima relazione fondamentale della Goniometria. Quindi possiamo dire che i lati dei nostri due triangoli sono proporzionali. Per visualizzare tutti i corsi.

La seconda relazione fondamentale della goniometria mette in relazione il seno ed il coseno di un angolo con la tangente dello stesso. Goniometria Funzioni goniometriche relazioni fondamentali e grafici. Goniometria Le cinque relazioni fondamentali v 19 2012 - wwwmatematikait 1 di 1 dimostrazioni. FORMULARIO DI GONIOMETRIA o Prima relazione fondamentale della goniometria cos.

Quindi la prima relazione fondamentale della goniometria è una relazione che lega il seno. Per dimostrarla si consideri la circonferenza goniometrica sia P il punto associato allangolo α il segmento AT corrisponde alla tangente goniometrica. La tangente di un angolo è data dal rapporto tra il suo seno e il suo. La somma dei quadrati del seno e del coseno di uno stesso angolo è uguale allunità.

Wwwmatematikait 1 di 1 grafici delle funzioni goniometriche seno coseno tangente cotangente definizione delle. Quindi la prima relazione fondamentale della goniometria è una relazione che lega il seno e il coseno di uno stesso angolo. Nacque nellantichità per viaggiare orientandosi con la posizione del Sole o delle. Da cui si ricava la prima relazione fondamentale della goniometria sen2 α cos2 α 1 A y x R 1 B α O C Volendo rappresentare graficamente le variazioni delle fun-zioni seno e coseno su.

La relazione fondamentale della goniometria o identità fondamentale della goniometria è una equazione che mette in relazione i quadrati del seno e del coseno di un. La prima relazione fondamentale della trigonometria si dimostra facilmente con il teorema di Pitagora. Si veri cano tre relazioni tra le funzioni che sono dette Relazioni fondamentali. Ogni funzione goniometrica ha una propria relazione matematica tra lampiezza dellangolo orientato e linsieme dei numeri reali.

Relazione fondamentale della goniomeria. Prima relazione fondamentale Prima relazione fondamentale Lega fra loro il seno ed il coseno permettendo di trasformare luno nellaltro Consideriamo una circonferenza trigonometrica. La prima relazione fondamentale della goniometria la prima relazione fondamentale della goniometria afferma che per qualsiasi angolo vale la seguente formula. Prima relazione fondamentale della goniometria.

Valgono le seguenti relazioni. Questa è la prima relazione fondamentale della goniometria. Nella circonferenza goniometrica il seno il coseno e il raggio formano un triangolo. In base ad essa sappiamo che la SOMMA dei QUADRATI del.

Sen o Seconda relazione fondamentale della goniometria. Formula e dimostrazione mediante circonferenza goniometrica e mediante il teorema di Pitagora. OH Ora osserviamo che. La somma dei quadrati di seno e coseno di un medesimo angolo è pari ad 1.

Prima relazione fondamentale della goniometriapdf. Un esempio pratico Prendo in considerazione un punto P. OA HP. Da quanto visto nellesempio precedente possiamo calcolare il seno dellangolo usando la prima.

AT non è altro che la tangente dellangolo α. In particolare questa afferma che la. Prima relazione fondamentale della goniometria. Seconda relazione fondamentale della goniometria.

Sia x2R allora cos2x sin2x 1.

Video Tutorial Di Matematica Relazioni Fondamentali Della Goniometria Youtube

Dieci Quesiti Al Volo Di Trigonometria Parte Ii

Equazioni Goniometriche Con Somma Di Angoli

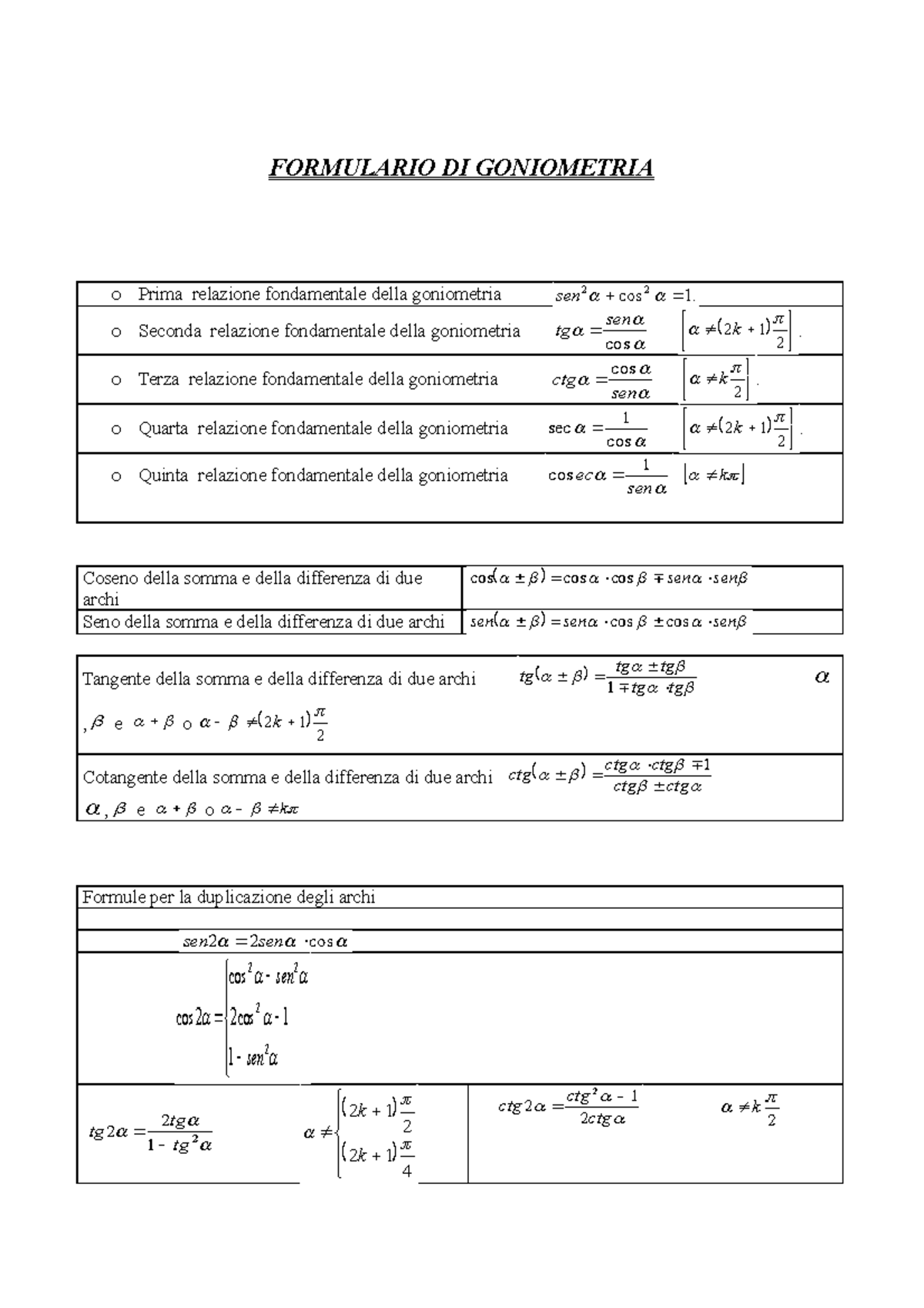Appunti Analisi Matematica Formulario Di Goniometria Formulario Di Goniometria O Prima Studocu

Esercizi Extra Formula Fondamentale Della Trigonometria Schemi Di Matematica